Acceptance Sampling Optimization using Least Number of Samples 

AQL, RQL, LTPD, type 1 error, type 2

 

 

Learn the probability of accepting in reference to fraction defective, at the most feasible way. 

 

 

Project Work 

 

In the single sampling plans for attribute data, acceptance-sampling plans can be created with the reference to Operating characteristic Curve. This OC curve basically plots the data of probability of accepting in reference to fraction defective. Since our study is regarding attributes and binomial data, we will use binomial distribution characteristics to calculate probability of acceptance. (Montgomery 2013) 

 

We draw OC curve in accordance to our lecture book Montgomery 2013, in order to obtain the same graphs. By this way, we can conclude and check that our graph is accurate or not.

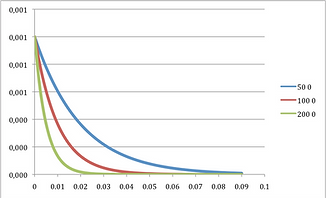
In ideal case, ideal OC curve must be a vertical line on lot fraction defective, where it is only possible by checking out and measuring all the population. However, it is impossible in most cases and not feasible nor rentable in any case. Therefore, we are almost always subject to work with samples. In all graph in this section x axis denotes fraction defective and y axis probability of acceptance (Pa), calculated as in the above formula 15.

Thus, let us begin with figuring out the effect of sample size (Similar to figure 15.4 in Montgomery 2013). 

 

 

Results  

For attribute data, we mostly need samples to figure out and conclude and comment on whole population. In most cases, basic sample size determination methods are used to determine the sample size by taking into account essentially the power of test, Beta (type-II) and alpha type-I errors.

Instead, we learnt how to use sequential sampling by increasing data points each case, and continue data collection if we are not out of type one and type –II errors. Therefore, we need to be convinced on AQL, RQL (LTPD, LQL) and alpha and Beta. Then, we increase the sample size until we reach AQL using binomial or hyper-geometric distribution.